调节阀被广泛用作汽、水流量控制系统的执行组件,其工作性能的好坏,直接影响控制质量的优劣,由于调节阀在不同使用场合安装方式不同和管路系统结构的变化以及工作介质的不同,使得调节阀工作条件变化较大,引起压降比显著降低,这时阀的工作流量特性与其固有特性相差很大引起特性畸变,这种畸变给控制系统的设计带来了困难,也会严重影响控制系统的性能指标。调节阀流量特性补偿的算法是实现流量特性补偿的关键。
调节阀的发展方向是模块化、精小型、智能型、总线型和标准化,国内对调节阀流量特性的补偿主要采用专为调节阀设计的控制器,研究调节阀流量特性补偿模块符合调节阀技术的发展方向,也有实际应用价值。
1 调节阀的流量特性及应用
1.1 定义
调节阀的流量特性是指介质流过调节阀的相对流量与相对位移(即阀的相对开度)之间的关系,数学表达式为:
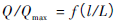 (1)
(1)
式中:Q/Qmax—相对流量,调节阀某一开度时流量Q与全开时流量Qmax之比;
l/L—相对位移,调节阀某一开度时阀芯位移l与全开时阀芯位移L之比。
1.2 理想流量特性
所谓理想流量特性是指调节阀前后差一定时的流量特性,它是调节阀的固有特性,由阀芯的形状所决定。理想流量特性主要有等百分比、抛物线、直线及快开等四种(图1)。
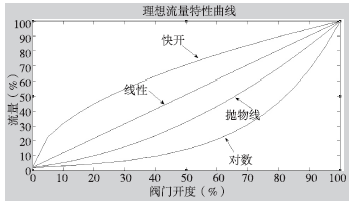
图1 理想流量特性曲线
直线流量特性是指调节阀的相对流量与相对位移成直线关系,即单位相对行程变化引起的相对流量变化是一个常数。
线性流量特性的数字表达式为:
 (2)
(2)
等百分比流量特性(对数流量特性)是指单位相对位移变化所引起的相对流量变化与此点的相对流量成正比关系。用数字表达式为:
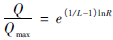 (3)
(3)
抛物线流量特性是指单位相对位移的变化所引起的相对流量变化与此点的相对流量值的平方根成正比关系,该特性介于直线特性与等百分比特性之间,使用上常以等百分比特性代之,其数学表达式为:
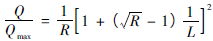 (4)
(4)
快开流量特性是指调节阀在开度较小时就有较大流量,随着开度的增大,流量很快就达到较大;此后再增加开度,流量变化很小。其数学表达式为:
 (5)
(5)
1.3 调节阀的可调比
调节阀的可调比R是指调节阀所能控制的较大流量Qmax和最小流量Qmin之比,即
R=Qmax/Qmin (6)
一般Qmin为较大流量的2%~4%,因此理想可调比的取值范围在25~50之间。可调比反映了调节能力的大小,因此希望可调比大一些为好。但由于阀芯结构设计和加工的限制,理想可调比一般不会太大,目前我国调节阀的理想可调比只要有30和50两种。
为了更好的研究调节阀的流量特性曲线,使得对畸变曲线进行校正后,能更加直观的进行分析,下面列出了当R分别取30,对应的理想流量特性数据,供参照(表1、图2)。
表1 流量特性的相对开度和对应流量(R=30)

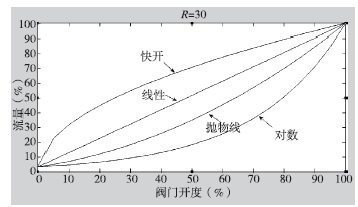
图2 R=30对应的四种理想流量特性曲线
2 补偿算法的介绍
本设计的流量特性补偿算法是基于二分法求零点的原理,二分法求零点的原理是:对于一个必有解的f(x)=0方程,可构造y=f(x)的函数,设y1=f(x1)<0,y2=f(x2)>0,则以(x1,y1),(x2,y2)两点作直线,交于x轴一点(x3,0),若y3=f(x3)>0,则以(x1,y1),(x3,y3)两点作直线,否则以(x3,y3),(x2,y2)两点作直线,交于x轴一点(x4,0),重复以上步骤,直到|yi=f(xi)-0|达到要求的精度范围。此时所求的xi的值即为f(x)=0的解,对二分法求零点的介绍是为了让读者更好的理解补偿算法,下面结合图3即对该算法进行详细介绍:
1)初始化LH=Lmax(阀门达到的最大开度),LL=Lmin(阀门达到的最小开度),QH=Qmax(流量计达到的最大流量,一般对应最大开度),QL=Qmin(流量计达到的最小流量,一般对应最小开度)。
2)采集给定的阀门开度值L0,根据已经保存的理想流量特性函数算出应达到的理想流量值Q0,输出L0,通过流量计采集实际的流量值Q1。
3)若|Q1-Q0|>error(error值决定补偿达到的精度,视实际情况而定),则进行步骤4,否则跳出补偿。
4)若Q1>Q0时,则LH=L0,QH=Q1,否则LL=L0,QL=Q1,计算出公式:
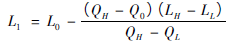
输出L1,通过流量计采集实际的流量值Q1。
5)返回步骤(3)。算法会在(3),(4),(5)步骤中循环,直到Q1与Q0之间的差值小于预设的值rand时完成补偿(图3)。
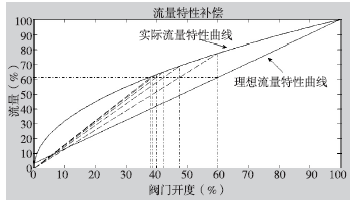
图3 补偿算法的实现和应用
本设计中算法采用MATLAB来实现,下面对该算法一些例程进行介绍。
3.1 求某点对应理想流量特性值补偿函数
function[L,sum]=dotcompensation(l)
该函数功能是对某一开度进行补偿,输入参数为要补偿的开度值(百分数),返回的参数为补偿后实际输出的开度值(百分数)和在该点进行补偿的运算次数。改变f1和f2,可以改变理想流量特性和实际流量特性。函数中有很多画图的操作,目的是方便仿真分析时对补偿过程的观察。
如图4所示,[Lsum]=dotcompensation函数,首先定义理想流量特性函数:
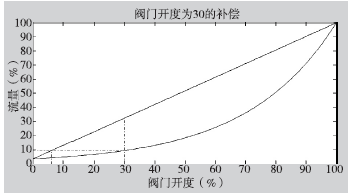
图4 阀门开度为30的补偿过程
f1=exp((x(i)-1)*log(R))(R为理想可调比),实际流量特性函数为:
f2=1/R+(1-1/R)*x(i)
此时理想流量为对数特性,实际流量为线性,
l=30时,得到[Lsum]=[6.1206 1]。
3.2 求对全区间流量特性补偿函数
function[L,sum]=linecompensation(float)
该补偿函数对全区间进行补偿,从而可以观察到补偿的整体效果,该补偿函数的输入参数是补偿达到的精度,如0.05,则补偿出来的效果理想流量与理想流量的差值不超过0.05,输出参数为两个数组,L为0到100这些整数点上进行补偿后实际输出的开度,sum为对这些点补偿的运算次数。
以畸变函数为凹函数为例,令理想流量特性曲线的函数表达式为:
f1=1/R+(1-1/R)*x
实际流量特性曲线的函数为
f2=1/R*(1+(sqrt(R)-1)*x)^2(凹函数),分析此种情况下的补偿过程,当float=0.05时,如图5所示。
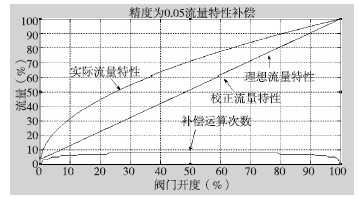
图5 精度为0.05时流量特性补偿
4 总结
本设计详细介绍了关于流量补偿算法的研究,无论是在生活还是在工业生产上,调节阀都被大量使用,难以避免地,在使用过程中会遇到流量特性畸变的问题,所以关于流量特性补偿算法的研究是很有意义的。该算法具有如下特点:
1)易编程实现,灵活,移植性强;
2)对于各种流量畸变特性都能够很好的校正过来,能够适应工业现场复杂多变的情况;
3)该算法除了能校正调节阀的流量特性曲线畸变外,还能按特殊需要而设计的流量特性曲线工作;
4)精度可调,但精度越高,补偿时间越长,需视具体情况而定。
同时,该算法也存在不足,如该算法对流量的采集有一定要求,当调节阀在使用时流量采集的信号会产生波动,同时当阀门动作时,流量达到稳定需要一定的时间,如3s~6s,严重影响补偿时间,为解决该问题,可以结合查表法,在流量稳定的时候,预先存一些阀门开度和其对应的流量值,在下次补偿时可以使用这些数据来尽量缩短补偿时间。本设计属于仿真研究,未经过实际测试,实际使用中可能还存在一些问题,留待作进一步的研究。